最近用一个多月的时间看完了 Michael Collins 的 Natural Language Processing 课程视频。视频只有前面一小部分有英文字幕，后面连字幕也没有。。还好基本能听懂。Collins 大牛讲得深入浅出、耐心细致，非常适合用来入门nlp。

写下这个小结当作学习笔记吧。

涉及的nlp问题

整个课程围绕着几个典型的nlp问题展开讨论，讲解的算法多种多样，但目标都是去更好地解决这些经典问题。

语言模型

语言模型可以给出一个单词序列在某一语料库的背景下出现的概率，它用来估计一个单词序列有多少概率在语料库代表的语言环境中出现。

即学习一个概率分布p，代表句子出现的概率，满足 $\sum\limits_{x\in V} p(x)=1 \ ,p(x)\geq0$ ，其中 $V$ 是无限大的字符串集合。

常用的是简单的n元语法模型，它是用 Markov 假设简化的概率。例如用 Second-Order Markov 假设得到的三元语法模型如下：

\begin{aligned} &P(X_1=x_1,X_2=x_2,...X_n=x_n)\\ =&P(X_1=x_1)\times P(X_2=x_2|X_1=x_1)\times ...\times P(X_n=x_n|X_1=x_1,...X_{n-1}=x_{n-1})\\ \approx& \prod\limits_{i=1}^n P(X_i|X_{i-1}=X_{i-1},X_{i-2}=x_{i-2}) \end{aligned}

定义 $X_0=X_{-1}=*$ ， $*$ 是起始符号。

标注

标注是给句中的每个单词分配一个标签，课程涉及的是词性标注（POS）和命名实体识别（NER）。

其中，NER是这样转化为标注问题的（引用PPT中的例子）：

Profits/NA soared/NA at/NA Boeing/SC Co./CC ,/NA easily/NA topping/NA forecasts/NA on/NA Wall/SL Street/CL ,/NA as/NA their/NA CEO/NA Alan/SP Mulally/CP announced/NA first/NA quarter/NA results/NA ./NA NA = No entity SC = Start Company CC = Continue Company SL = Start Location CL = Continue Location

Parsing

Parsing 是解析句子的结构，课程讨论了句法分析和依存句法分析。

句法分析

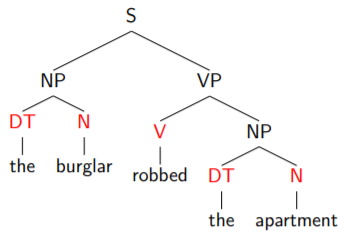
无标签的依存句法分析（每条弧指向单词的修饰，弧上没有标签）

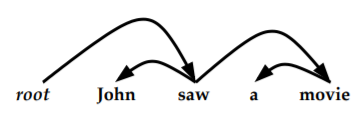
算法

课程介绍了多种算法来解决上述问题，其中的每一大类算法往往可以用于解决多个问题。我这里以算法为线索来介绍。

线性插值与打折算法

线性插值和打折算法可以用来解决n元语言模型的数据稀疏问题。

例如，对于三元语法，由于三元组的组合很多，而数据有限，有些三元组的计数非常少或者为0，这会导致包含这个三元组的句子的概率非常小，偏离实际情况。

线性插值

线性插值将几种n元语法线性混合：

\begin{aligned} q(w_i|w_{i-1},w_{i-2})= & \lambda_1 \times q_{ML}(w_i|w_{i-1},w_{i-2}) \times \\ & \lambda_2 \times q_{ML}(w_i|w_{i-1}) \times \\ & \lambda_3 \times q_{ML}(w_i) \\ where\ \lambda_1+\lambda_2+\lambda_3=1, and\ \lambda_i\geq0 \ for\ all\ i \end{aligned}

可以证明，混合后的语言模型是一个概率分布。 $\lambda$ 的取值可以由模型在验证集上的似然确定。

打折算法

一些低频三元组的出现概率可导致其频率计数总是记为0，比如当其概率远小于三元组数量的倒数时。这是可以将其它三元组的概率扣掉一部分，按某种比例分配给计数为0的三元组。

Katz Back-Off 的二元组模型将计数大于0的二元组的计数打折，匀出的概率按一元组的计数分配给计数等于0的二元组。类似地，Katz Back-Off 的三元组模型将计数大于0的三元组的计数打折，匀出的概率按上述的二元组计数分配给计数等于0的三元组。

Markov 过程与 Viterbi 算法：求解序列标注问题

Markov 过程与 Viterbi 算法是息息相关的。Markov 假设将问题简化，往往使其具有动态规划问题的性质。而求解这类问题的动态规划算法就叫 Viterbi 算法。

Markov 过程

对于一个随机变量序列 $X_1,X_2,...,X_n$ 。如果 $p(X_i=x_i|X_1=x_1,X_2=x_2,...,X_{i-1}=x_{i-1})=p(X_i=x_i|X_{i-1}=x_{i-1})$ ，称为一阶 Markov 过程。如果 $p(X_i=x_i|X_1=x_1,X_2=x_2,...,X_{i-1}=x_{i-1})=p(X_i=x_i|X_{i-2}=x_{i-2},X_{i-1}=x_{i-1})$ ，称为二阶 Markov 过程。即第i个随机变量的取值只与其之前若干个随机变量的取值相关。这里已经能感受到和动态规划算法的联系了。

Hidden Markov Model

Hidden Markov Model 定义了这样的过程：存在一组满足 Markov 假设的状态序列 $X_1,X_2,...,X_n$ ，每个状态对应一个输出，其概率分布满足 $p(y_i|x_i)=e(y_i|x_i)$ ，于是得到了一个观察序列 $Y_1,Y_2,...,Y_n$

对于标注问题，我们可以这样假设，使它符合HMM：标注序列为HMM的状态序列，句子为HMM的观察序列，而 Morkov 状态转移的概率和输出概率是从训练集中学习得到的。那么标注的过程即为根据观察序列和HMM参数求解状态序列的过程，称为解码。

用于标注问题的 Trigram HMMs 定义为：

\begin{aligned} &p(x_1...x_{n+1},y_1...y_n)=\prod\limits_{i=1}^{n+1} q(x_i|x_{i-2},x_{i-1}) \prod\limits_{i=1}^{n} e(y_i|x_i) \\ &where\ x_0=x_{-1}=* , and\ x_{n+1}=STOP \end{aligned}

$x_1...x_{n+1}$ 是标注序列， $y_1...y_n$ 是句子。

Viterbi 算法

Viterbi 算法是一种动态规划算法，给定观察序列（句子）和HMM参数，它能找出概率最大的状态序列（标注序列）。这算是一个简单的动态规划问题了。

最优子结构定义为 $f(k,u,v)$ ，表示满足 $x_{k-1}=u,x_k=v$ 的前 $k$ 个状态序列能获得的最大概率。

状态转移方程为： $f(k,u,v)=\max\limits_{w\in S_k-2} f(k-1,w,u)q(v|w,u)e(y_k|v)$ $S_{k-2}$ 是 $X_{k-2}$ 的取值集合。

标注问题的HMM参数估计

可以用语言模型中所用的线性插值和打折算法。

对于低频词，有更好的办法————根据单词的拼写特征，把它们归入一些大类中。

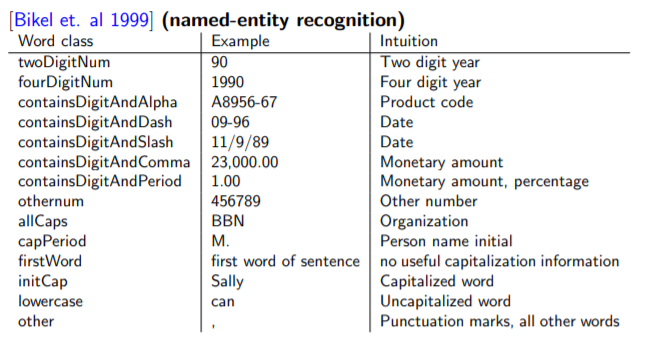
概率上下文无关语法（PCFG）与 CKY 算法：求解句法分析问题

通过POS，我们可以得到句子中每个单词对应的词性序列。如果定义出一组从起始符号推导出词性序列的语法规则，就可以用语法分析算法构建 parsing tree。

但与编程所用的 CFG 不同，自然语言存在着大量的歧义，因此，学者提出了概率上下文无关语法（PCFG）。而选择出一组推导方案，使句子的出现概率最大的算法之一是CKY算法，同样是一种DP算法。

概率上下文无关语法

PCFG为每条推导规则定义了概率。

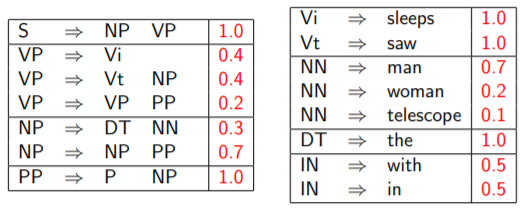
CKY 算法

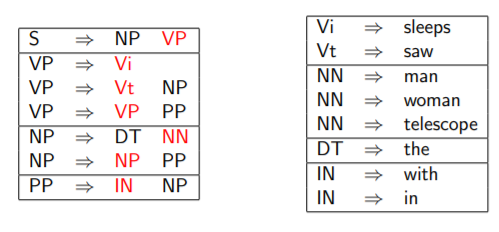
CKY 算法能找出一组推到规则，使生成句子的概率最大。它要求所用的 CFG 符合 Chomsky 标准形式，它要求推导规则为以下两种形式之一：

$X\rightarrow Y_1Y_2$ ，其中 $Y_1,Y_2$ 是非终结符。
$X\rightarrow Y$ ，其中 $Y$ 是终结符。

显然，PCFG都可以转化为上述 Chomsky 标准形式。

CKY 算法是动态规划算法，思想类似矩阵连乘积。

问题的最优子结构 $f(i,j,X)$ 表示非终结符 $X$ 生成句子子串 $x_i...x_j$ 的最大概率。

状态转移方程： $f(i,j,X)=\max\limits_{X\rightarrow YZ\in R,s \in \{i...i-1\}} q(X\rightarrow YZ)f(i,s,Y)f(s+1,j,Z)$

Lexicalized PCFGs

PCFG 处理不好短语的附着问题，因为改变短语的修饰对象往往不影响句子的概率。

Lexicalized PCFGs 给语法规则引入了更多的语义信息，从而提高精确度。

Lexicalized PCFGs 为每个推导规则指定了一个 head ，作为规则的中心成分。左侧的非终结符会继承右侧标记为 head 的非终结符的语义标记（一个单词）。

于是，句子的语法树扩充成了下图：

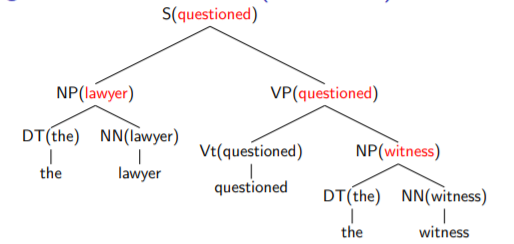
非终结符也需要被扩充，加上语义标记（非终结符对应的句子中的某个单词）的修饰了。如 $S(saw) \rightarrow_2 NP(man) VP(saw)$ ，箭头的下标2表示右侧的第二个非终结符是 head。

Lexicalized PCFGs的参数成倍的增加了，因此用下面的假设来估计参数：

\begin{aligned} &q(S(saw) \rightarrow_2 NP(man) VP(saw)) \\ =&q(S \rightarrow_2 NP\ VP | S,saw) \times q(man | S \rightarrow_2 NP\ VP ,saw)\\ =&(\lambda_1 \times q_{ML}(S \rightarrow_2 NP\ VP | S,saw) \times \lambda_2 \times q_{ML}(S \rightarrow_2 NP\ VP | S)) \times \\ &(\lambda_3 \times q_{ML}(man | S \rightarrow_2 NP\ VP ,saw) \times \lambda_4 \times q_{ML}(man | S \rightarrow_2 NP\ VP) \times \lambda_5 \times q_{ML}(man|NP)) \end{aligned}

Lexicalized PCFGs 同样使用 CKY 算法求解推导规则。

Log-Linear Models

Log-Linear Model 是一类概率预测模型，它假设（样本，类别）元组的特征向量与参数向量的内积与分类正确的概率的对数值成正比。

由于这是机器学习的经典算法，这里关注模型的思想，然后介绍在 nlp 领域的应用。

Log-Linear Models 与最大熵模型

Log-Linear Models 定义了特征函数 $f$ 和参数向量 $v$ ，做出如下假设： $p(y|x;v)=\frac{e^{v \cdot f(x,y)}}{\sum\limits_{y'\in Y}e^{v \cdot f(x,y')}}$

我们使用极大似然估计确定参数 $v$ ，对数似然函数为： $L(v)=\sum\limits_{i=1}^{n}\log p(y_i|x_i;v)$

似然函数看似复杂，梯度上升法求解 $v$ 的公式却比较简单：

对数似然模型也叫最大熵模型，它们是等价的。

最大熵模型寻找的是的是满足以下两个条件的 $p(y|x)$ 表达式：

对于每个特征，它对每个样本(x,y)的期望等于模型预测的该特征的期望 $\sum\limits_{x,y}\overline{p}(x,y)f_i(x,y)=\sum\limits_x \overline{p}(x)p(y|x)f_i(x,y)$
条件熵最大 $H(p)=-\sum\limits_{x}\overline{p}(x)\sum\limits_{y}p(y|x)\log p(y|x)$

条件1保证了从每个特征的角度看，模型的预测与训练集相符。这构成了一个方程组，我们希望用已知的 $\overline{p}$ 和 $f_i$ 来表达 $p(y|x)$ 。

但是 $x,y$ 的组合很多，导致条件1的方程组不足以确定全部的 $p(y|x)$ 。条件2限定只取条件熵最大的一组解。这实际上保证了只要特征相同，样本的概率分布就相同，模型不考虑样本除了特征以外的因素。

经过推导，以上两个条件的解正是 $p(y|x)=\frac{e^{v \cdot f(x,y)}}{\sum\limits_{y'\in Y}e^{v \cdot f(x,y')}}$ ， $v$ 是使 $L(v)=\sum\limits_{i=1}^{n}\log p(y_i|x_i;v)$ 最大化的向量，这就是对数似然模型的两个式子，因此两者是等价的。

因此，对数似然模型的假设 $p(y|x)=\frac{e^{v \cdot f(x,y)}}{\sum\limits_{y'\in Y}e^{v \cdot f(x,y')}}$ ，隐含了这样的假设：样本集的每个特征的期望 $\mathrm{E}_{f_i}$ 就是预测对象的期望，并且除了这些特征外，没有其他影响分类的因素。

这样的假设太强了，在实际问题中难以达到。因此，很多只对 $p(y|x)$ 的形式作出假设，并用极大似然解出参数的模型，也能取得很好甚至更好的表现。

正则化

如果在训练集中，具有某一特征 $f_i$ 的样本都属于同一类，那么 $v_i$ 会趋于无穷大，这是不合理的。因此，引入了新的假设——参数 $v$ 服从均值为0的高斯分布。

于是，似然函数增加了正则项： $L(v)=\sum\limits_{i=1}^{n}\log p(y_i|x_i;v)-\frac{\lambda}{2}\sum\limits_{k=1}^m v_k^2$

用于标注的 Log-Linear Models：最大熵 Markov 模型（MEMMs）

我们使用与之前的 HMM 模型相似的独立性假设：

\begin{aligned} p(t_{[1:n]}|w_{[1:n]})= & \prod_{i=1}^n p(t_i|t_{[1:i-1]},w_{[1:n]}) \\ =& \prod_{i=1}^n p(t_i|t_{i-2},t_{i-1},w_{[1:n]}) \end{aligned}

而 $p(t_i|t_{i-2},t_{i-1},w_{[1:n]})$ 可以使用 Log-Linear Models 来估计。定义四元组 $<t_{i-2},t_{i-1},w_{[1:n]},i>$ 为历史，模型根据每个位置上的历史来预测该位置标签的概率分布。

对于POS标注，可以这样定义特征：

用于 MEMM 的 Viterbi 算法也与 HMM 模型的非常类似，不再讨论了。实际上，这一模型只是替换了 HMM 中预测 $p(t_i|t_{i-2},t_{i-1},w_{[1:n]})$ 的方式，允许引入更丰富的特征。

计算细节 由于前后几个单词的任意组合被包含在特征中，特征的数量是非常大的， $v$ 的计算复杂度非常高。实际上，由于是稀疏的01特征，一个样本 $(x,y)$ 只有少数特征是为1的。我们不用显式地计算出样本的特征向量 $f$ ，只需确定 $f$ 的哪些位置为1即可。

用于 Parsing 的 Log-Linear Model：Ratnaparkhi’s Parser

Ratnaparkhi 把语法树表示为一系列的决策序列。模型根据句子和全部的历史决策来预测下一个决策的概率分布。由于预测是基于从全部的历史决策提取的特征，因此无法应用动态规划算法，而是使用 beam search 这种启发式搜索算法。

Global Linear Models

上述ME模型为序列的每个位置提供了概率分布，然后用 Viterbi 算法解码，这就很难引入跨越多个位置的特征。如果将整个输入序列和可能的分类序列一起输入模型，则可以利用更宏观的特征来预测，这就是全局线性模型。

GLMs 的组成

一个 GLM 由三部分组成：

函数 $f(x,y)$ 将整个输入和分类组成的元组映射为特征向量。
函数 $GEN(x)$ 生成输入序列 $x$ 对应的可能的分类序列的集合。
参数向量 $v$ 。

模型输出为最可能的分类序列：

F(x)=argmax_{y\in GEN(x)} f(x,y)\cdot v

初看这个公式，想到需要回答一些问题：

如何生成潜在的分类序列集合？
上述集合可能很大时，如何有效率地找到最优解 $y$ ？

可以把 $GEN(x)$ 定义为寻找可行解的算法，或者 baseline 模型的前n个最优解。而如果集合很大，通过巧妙地定义 $f$ ，我们可以高效地解出 $F$ ，后面会进行论述。

用于 Parsing Reranking 的 GLMs

Reranking 已经表明 $GEN(x)$ 的定义了，例如 Lexicalized PCFG 预测概率最大的前25个 Parse。由于潜在的 $y$ 不多， $f$ 可以包含各种全局特征，直接计算即可。

可以使用感知机算法的变种来估计 $v$ ：

用于标注的 GLMs

这个问题中的 $GEN(x)$ 可以对应所有的标签序列，但通过定义 $f(x,y)$ ，我们不用显示地枚举每一个 $y$ 。

仿照 MEMMs 中的定义，我们以 $<t_{i-2},t_{i-1},w_{[1:n]},i>$ 为历史 $h_i$ ，定义每个位置上的局部特征为 $g(h_i,t_i)$ ， $g$ 是与 MEMM 的特征函数类似的局部特征函数，定义全局特征函数：

f(w_{[1:n]},t_{[1:n]})=\sum\limits_{i=1}^n g(h_i,t_i)

于是：

\begin{aligned} F(x)=&argmax_{y\in GEN(x)} f(x,y)\cdot v \\ =&argmax_{t_{[1:n]}\in GEN(w_{[1:n]})} \sum\limits_{i=1}^n g(h_i,t_i)\cdot v \\ \end{aligned}

由于 $g(h_i,t_i)$ 只依赖于前两个位置的标签，这里再次可以应用DP算法。

用于依存语法分析的 GLMs

依存语法分析构造了一棵有 $n+1$ 个节点的语法树（以起始符号为根）。定义：

f(x,y)=\sum\limits_{(h,m)\in y}^n g(x,h,m)

$(h,m)$ 是位置h指向位置m的一条边。

那么：

\begin{aligned} F(x)=&argmax_{y\in GEN(x)} f(x,y)\cdot v \\ =&argmax_{y\in GEN(x)} \sum\limits_{(h,m)\in y}^n g(x,h,m)\cdot v \\ \end{aligned}

这个问题恰好可以用最大生成树算法解决。特别地，如果规定对于每个词，它只被它的某个领域内的所有词修饰，即分析结果中不存在交叉的弧，那么 $F$ 可以用类似 CKY 的 DP 算法解决。